Преобразование чисел между любыми системами счисления онлайн

Для тех, кому нужен более продвинутый конвертер, доступны варианты с дополнительными функциями, такими как преобразование между менее распространенными основаниями или работа с большими числами. Однако для

См. также

В этом разделе вы найдете дополнительные ресурсы, которые помогут вам лучше понять числовые преобразования и их практическое применение. Мы рассматриваем различные методы и инструменты, уделяя особое внимание эффективным методикам и широко используемым форматам чисел.

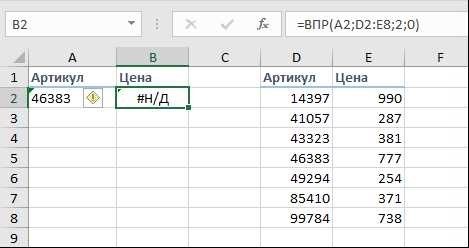
Узнайте, как каждая цифра играет решающую роль при переводе из восьмеричного в шестнадцатеричный формат. Наш специализированный калькулятор обеспечивает стопроцентную точность даже при работе со сложным кодом. Если вы работаете с текстовым форматом, наш конвертер, выделенный зеленым цветом, гарантирует, что каждая цифра и ячейка будет введена с точностью.

Часто пользователям приходится переключаться между десятичным и другими форматами. Здесь мы рассказываем о наиболее часто используемых конвертерах, таких как инструмент преобразования десятичной системы в шестнадцатеричную, обеспечивающий высокую степень точности. Кроме того, вы узнаете об особенностях работы с текстом в виде чисел и о том, как наши инструменты упрощают эти преобразования.

Ознакомьтесь с нашими ресурсами о том, как эффективно преобразовывать код с помощью повторяющихся шагов и удобных интерфейсов. Будь то преобразование текстовой строки или числового ввода, наши руководства предлагают полное понимание процесса.

P.S.: Приведенные ссылки тщательно подобраны, чтобы помочь вам на каждом этапе процесса преобразования, обеспечивая бесперебойность и точность каждой операции.

Базовый конвертер — как перевести двоичное число в десятичное

Процесс преобразования двоичного числа в десятичный формат необходим в различных областях вычислительной техники и математики. Этот базовый конвертер помогает преобразовать двоичные значения в их десятичные аналоги с помощью простого метода. Ниже описано, как это сделать с помощью простых шагов.

Каждая цифра двоичного числа имеет соответствующее значение в десятичной системе. Умножив каждую двоичную цифру на силу 2 (основание) в соответствии с ее положением и просуммировав результаты, можно получить десятичный эквивалент. Этот процесс, хотя и ручной, эффективен и часто требуется при работе без автоматизированных инструментов.

Шаг	Действие	Результат
1.	Возьмите двоичное число (например, 1101) и запишите его цифры.	Двоичное число: 1101
2.	Присвойте каждой цифре силу 2, начиная с 0 справа.	1×2 3, 1×2 2, 0x2 1, 1×2 0
3.	Вычислите значение каждой двоичной цифры в зависимости от ее положения.	8, 4, 0, 1
4.	Просуммируйте все вычисленные значения.	8 + 4 + 0 + 1 = 13
5.	Проверьте полученное десятичное число.	Десятичное число: 13

Выполнив эти действия, вы сможете легко перевести двоичные числа в десятичный формат с помощью этого базового конвертера. Этот метод также применим при переводе двоичных чисел в другие базы, такие как шестнадцатеричная или восьмеричная, путем соответствующей корректировки базы. В результате получается точное преобразование, обеспечивающее ясность при решении различных вычислительных задач.

P.S.: Всегда перепроверяйте свои вычисления, особенно когда имеете дело с длинными двоичными последовательностями, чтобы убедиться в точности результатов.

Конвертер оснований — как преобразовать шестнадцатеричное число в десятичное

Преобразование шестнадцатеричной системы счисления в десятичную предполагает перевод чисел из одного основания в другое. В данном случае мы рассмотрим, как эффективно выполнить это преобразование. Шестнадцатеричная система использует формат основания 16, в то время как десятичная система оперирует основанием 10. Понимание этого преобразования позволит вам легко работать с различными числовыми представлениями.

Вот пошаговый подход к преобразованию шестнадцатеричного числа в его десятичный эквивалент:

Начните с определения каждой цифры в шестнадцатеричном числе. Например, шестнадцатеричное число 1A3F состоит из цифр 1, A, 3 и F.
Присвойте каждой шестнадцатеричной цифре десятичное значение. В шестнадцатеричном исчислении цифры варьируются от 0 до 9, а буквы от A до F, где A обозначает 10, B — 11 и так далее до F, которая равна 15.
Умножьте каждую цифру на 16, возведенную в степень ее положения, считая справа налево, начиная с 0. Например, в 1A3F:

F (15) находится в позиции 16 0
3 находится в позиции 16 1
A (10) находится в позиции 16 2
1 находится в позиции 16 3

Вычислите десятичное значение, суммируя эти произведения:

F (15) * 16 0 = 15
3 * 16 1 = 48
A (10) * 16 2 = 2560
1 * 16 3 = 4096

Сложите эти результаты, чтобы получить десятичное число:

15 + 48 + 2560 + 4096 = 6719

Советуем прочитать: Как найти владельца недвижимости по кадастровому номеру бесплатно

Используя этот метод, вы можете точно преобразовать шестнадцатеричные значения в десятичные. Чтобы упростить этот процесс, вы можете воспользоваться инструментом конвертации оснований, доступным в различных калькуляторах или программных приложениях. Если же вы предпочитаете ручные расчеты, то выполнение описанных выше действий обеспечит точный результат. За дополнительной помощью обратитесь к онлайн-ресурсам или калькуляторам, специально разработанным для преобразования оснований.

p.s. Если вы имеете дело с другими системами счисления, например двоичной или восьмеричной, то здесь действуют аналогичные принципы с поправками на базовые значения.

Конвертер оснований — как перевести восьмеричное число в десятичное

Понимание процесса преобразования восьмеричной системы счисления в десятичную может значительно расширить ваши возможности работы с различными системами счисления. Это преобразование позволяет трансформировать значения из одного числового формата в другой, давая представление о том, как различные основания взаимодействуют друг с другом. Придерживаясь систематического подхода, вы сможете эффективно переводить восьмеричные значения в их десятичные аналоги.

Чтобы преобразовать восьмеричное число в десятичное, нужно использовать специальную формулу, которая предполагает умножение каждой цифры восьмеричного числа на соответствующую ей степень 8 и суммирование результатов. Например, возьмем восьмеричное число 345. Чтобы перевести его в десятичную систему счисления, нужно вычислить:

Здесь 8 2 означает 64, 8 1 — это 8, а 8 0 — это 1. Вычисления выполняются следующим образом:

3 * 64 + 4 * 8 + 5 * 1 = 192 + 32 + 5 = 229

Таким образом, десятичный эквивалент восьмеричного числа 345 равен 229. Этот метод обеспечивает точное преобразование восьмеричных значений в их десятичные формы, позволяя вам легко работать в различных системах счисления.

Для более эффективного подхода воспользуйтесь онлайн-конвертером базы. Эти инструменты автоматизируют процесс преобразования и исключают ручные расчеты, обеспечивая точность и экономя время. При использовании такого инструмента просто введите восьмеричное число в указанную ячейку, и конвертер выдаст вам десятичный эквивалент.

Таким образом, перевод из восьмеричной системы счисления в десятичную предполагает применение формулы преобразования оснований. Независимо от того, используете ли вы ручные расчеты или специализированный онлайн-конвертер, понимание процесса гарантирует, что вы сможете уверенно работать с числовыми значениями в различных основаниях.

p.s. Для дальнейшего обучения изучите дополнительные инструменты и калькуляторы, поддерживающие различные преобразования оснований, такие как двоичная, шестнадцатеричная и система base-12, чтобы повысить свой уровень владения числовыми манипуляциями.

Конвертер оснований — как перевести десятичную систему в двоичную

Понимание процесса преобразования между различными методами счисления необходимо в различных областях техники. В этом разделе мы рассмотрим метод перевода чисел из десятичной системы в двоичную. Эта процедура жизненно важна для таких задач, как программирование и проектирование цифровых схем. Использование правильных инструментов может значительно упростить эту процедуру.

Для начала вам необходимо знать основы двоичной и десятичной систем. Десятичная система, широко используемая в повседневной жизни, оперирует основанием 10, в то время как двоичная система использует основание 2. Для плавного преобразования обычно используется конвертер оснований, позволяющий вводить десятичное число и получать его двоичный эквивалент.

Вот простой подход к преобразованию десятичного числа в двоичное. Сначала возьмите десятичное число и разделите его на 2. Запишите остаток, который будет либо 0, либо 1. Этот остаток представляет собой наименьший значащий бит (LSB) в двоичном числе. Затем разделите полученное число на 2 и повторите процесс, записывая каждый остаток. Продолжайте эту процедуру до тех пор, пока коэффициент не достигнет 0. Окончательное двоичное число получается путем считывания остатков снизу вверх.

Для тех, кто предпочитает автоматизацию, существуют онлайн-конвертеры. Просто введите десятичное число в специальное поле ввода и позвольте инструменту сделать все остальное. Эти конвертеры эффективны и дают быстрые результаты. Они особенно полезны при сложных преобразованиях больших чисел.

Кроме того, многие специализированные инструменты предлагают такие функции, как история преобразования и опции форматирования, чтобы удовлетворить различные потребности. При использовании этих инструментов обязательно перепроверяйте результаты на точность. В образовательных целях также рекомендуется практиковать ручную конвертацию, чтобы лучше понять суть процесса.

Примечание: При работе с этими инструментами руководствуйтесь инструкциями для оптимального использования. Для получения дополнительной информации, перейдите по этой ссылке p.s. Экспериментируя с различными числами, вы лучше освоите процесс.

Особенности базового конвертера

Базовый конвертер представляет собой простой метод преобразования чисел между различными форматами. Понимание принципов его работы может значительно повысить вашу эффективность при работе с числовыми данными в различных базисах.

Вот некоторые ключевые аспекты базового конвертера:

Вход и Выход: Сначала вы вводите число в определенном формате. Затем инструмент обрабатывает этот ввод, чтобы получить результат в нужной базе. Например, введя число в двоичном формате, можно преобразовать его в десятичный, шестнадцатеричный или другие форматы.
Простота использования: Многие базовые конвертеры оснащены удобными интерфейсами, в которых достаточно ввести число, выбрать основание для преобразования и получить результат. Это позволяет переключаться между форматами с минимальными усилиями.
Поддерживаемые системы счисления: Базовые конвертеры обычно работают с различными системами счисления, включая двоичную, десятичную и шестнадцатеричную. Каждый формат имеет свой набор правил для представления чисел, и конвертер упрощает этот процесс, автоматизируя преобразование.
Точность и аккуратность: При использовании таких инструментов точность, как правило, сохраняется, что обеспечивает надежность результатов. Это очень важно для приложений, требующих точного представления чисел.
Функциональность копирования и вставки: Обычно можно скопировать результат непосредственно из конвертера и вставить его в другие документы или приложения. Эта функция облегчает интеграцию преобразованных чисел в отчеты или расчеты.

Ознакомившись с этими функциями, вы сможете эффективно использовать базовый конвертер для преобразования числовых данных. Работаете ли вы с преобразованиями десятичных чисел в двоичные, шестнадцатеричных в десятичные или другими, понимание этих ключевых аспектов гарантирует точность и бесперебойность работы.

100% бесплатно

Доступ к инструментам для преобразования между различными числовыми базами может быть очень полезен, особенно при решении разнообразных математических задач и задач программирования. Эти инструменты позволяют плавно переходить от одной базы к другой без каких-либо затрат. Они дают пользователям возможность быстро и эффективно выполнять преобразование оснований, используя как ручной ввод, так и автоматизированные решения.

Одним из эффективных подходов является использование конвертеров оснований, поддерживающих различные системы счисления, включая двоичную (основание-2), десятичную (основание-10), шестнадцатеричную (основание-16) и другие. Эти конвертеры обеспечивают простой способ преобразования значений, позволяя пользователям легко работать с различными основаниями. Например, вставляя число в указанное поле ввода, конвертер может отобразить результат в нужной базе.

Ниже приведен пример представления различных систем счисления:

Десятичная	Двоичная	Шестнадцатеричная	База-12
10	1010	A	A
255	11111111	FF	1F
100	1100100	64	84

В этих конвертерах часто можно выбрать входное и выходное основание и сразу же просмотреть результаты преобразования. Будь то образовательные цели, программирование или анализ данных, эти бесплатные инструменты представляют собой бесценный ресурс для удобной работы с различными системами оснований.

Преобразование чисел между различными системами оснований

В сфере цифровых вычислений преобразование значений из одной системы счисления в другую является фундаментальной операцией. Этот процесс заключается в переводе представлений из одной системы счисления в другую, что обеспечивает беспрепятственное взаимодействие между различными системами. Независимо от того, работаете ли вы с двоичной, десятичной, шестнадцатеричной или любой другой системой счисления, понимание этих преобразований необходимо для точного манипулирования данными.

Одним из эффективных инструментов для этой цели является конвертер оснований. Этот калькулятор позволяет вводить значения и автоматически преобразовывать их в нужную систему счисления. Например, чтобы перевести число из двоичной системы в десятичную или из десятичной в шестнадцатеричную, достаточно воспользоваться интерфейсом конвертера. Этот инструмент справляется с тонкостями преобразования, применяя математические операции, такие как умножение и деление, основанные на значении места и остатках.

При более практичном подходе можно выполнить преобразование вручную, разбив числа на столбцы и вычислив вклад каждой цифры в зависимости от ее основания. При этом используются такие методы, как позиционная нотация и отслеживание остатков, чтобы определить конечное значение в целевом основании.

Если вы предпочитаете наглядное пособие, многие конвертеры предлагают текстовое поле, куда вы можете вставить свое число и получить мгновенный результат в новой базе. Кроме того, некоторые продвинутые инструменты предоставляют пошаговое описание процесса конвертации, показывая, как каждая цифра и ее положение влияют на конечный результат.

Чтобы подробно изучить эти методы преобразования, ищите инструменты с интерактивными функциями и пошаговыми руководствами. Эти ресурсы помогут вам разобраться в тонкостях преобразования оснований и эффективно применять их для решения различных числовых задач.

Преобразование между различными системами счисления

Преобразование между различными системами счисления — распространенная задача в вычислительной технике и математике. Этот процесс включает в себя преобразование числа из одного представления в другое, что позволяет использовать его в различных контекстах или вычислениях. Для достижения точных и эффективных преобразований используются различные методы и инструменты.

Для примера здесь приведен обзор того, как можно выполнить эти преобразования:

Определите исходную систему: Определите исходное основание числа, которое может быть двоичным, восьмеричным, десятичным, шестнадцатеричным или другим. Например, в двоичных числах используется основание-2, а в шестнадцатеричных — основание-16.
Примените формулу преобразования: Используйте соответствующую формулу или метод для преобразования числа. Например, преобразование из двоичной системы в десятичную предполагает умножение каждой цифры на 2, возведенное в степень ее положения, и суммирование результатов.
Используйте инструменты для преобразования: В Интернете можно найти специализированные конвертеры и калькуляторы, которые упрощают этот процесс. Эти инструменты позволяют ввести число и мгновенно получить его представление в нужном основании.

При использовании онлайн-конвертеров или калькуляторов убедитесь, что они поддерживают конкретные базы, с которыми вы работаете. Например, преобразование из шестнадцатеричной системы счисления в десятичную включает в себя разные шаги по сравнению с преобразованием из десятичной системы счисления в двоичную. Многие инструменты обеспечивают 100-процентную точность, но при необходимости важно проверять результаты вручную.

Советуем прочитать: ВЦ Инкомус Пермь - Подача показаний счетчиков

Таким образом, преобразование чисел между различными системами счисления требует понимания основных принципов каждой системы и применения правильных методов или инструментов. Независимо от того, используются ли ручные расчеты или автоматические конвертеры, точность является ключевым фактором для получения надежных результатов.

Конвертер систем счисления

Конвертер систем счисления — это необходимый инструмент для преобразования чисел из одной системы счисления в другую. С его помощью вы можете легко переключаться между различными системами, включая двоичную, восьмеричную, десятичную и шестнадцатеричную. Процесс гарантирует, что каждая цифра будет правильно представлена и переведена в нужный формат с учетом различных систем оснований.

При работе с конвертером вы вводите число в определенной базе, а инструмент вычисляет его эквивалент в целевой базе. Например, двоичное число может быть преобразовано в десятичное или шестнадцатеричное. При этом каждая цифра переводится в соответствии с ее значением в конкретном основании, которое затем выражается в выбранном формате. Такое преобразование особенно полезно для программирования, анализа данных и различных вычислительных задач.

Чтобы воспользоваться конвертером, просто введите число в текстовое поле, выберите исходное и целевое основания и запустите процесс преобразования. Результат будет отображен в выбранной базе, что облегчит сравнение и анализ. Многие конвертеры также включают такие функции, как основание 12, основание 16 или даже пользовательские основания, обеспечивая гибкость для различных потребностей.

Кроме того, расширенные конвертеры позволяют работать с большими числами или выполнять вычисления с преобразованием оснований. Эта функциональность очень важна для задач, требующих точного представления чисел в разных системах. Например, конвертация из двоичной системы в десятичную или выполнение операций с восьмеричными значениями могут быть эффективно решены с помощью надежного конвертера.

Для оптимального использования убедитесь, что входное число правильно отформатировано и что выбранное основание соответствует ожидаемой системе. Такое внимание к деталям гарантирует точные результаты и способствует эффективному использованию конвертера в различных приложениях.

P.S. Если у вас возникнут проблемы или потребуется дополнительная настройка, многие конвертеры предоставляют дополнительные настройки или опции поддержки для улучшения функциональности и удобства использования. Изучите эти функции, чтобы полностью использовать возможности вашего конвертера систем счисления.

Наиболее часто используемые системы счисления

Понимание различных систем нумерации очень важно для решения различных задач в области вычислительной техники и цифровых технологий. Каждая система имеет свой набор правил и характеристик, что делает их подходящими для решения конкретных задач. Например, выбор системы влияет на то, как числа представляются, манипулируются и интерпретируются различными программными и аппаратными средствами. Когда вам нужно работать с этими системами, конвертер может стать бесценным инструментом. Он позволяет эффективно преобразовывать данные между различными системами, будь то программирование, обработка данных или простые вычисления.

Среди наиболее широко используемых систем — двоичная, десятичная и шестнадцатеричная. Двоичная система, или основание-2, является основополагающей в вычислениях, где каждая цифра представляет собой степень 2. Десятичная система, или основание-10, используется нами ежедневно и включает в себя цифры от 0 до 9. Шестнадцатеричная система, или основание-16, использует цифры 0-9 и буквы A-F, что делает ее удобной для компактного представления двоичных данных. Каждая из этих систем имеет свои особенности и преимущества в различных контекстах.

Для тех, кто часто работает с этими системами, конвертер или калькулятор может упростить процесс. Существует множество бесплатных онлайн-конвертеров для быстрого преобразования значений между системами. Подобные инструменты часто имеют удобный интерфейс, в котором можно вводить числа и получать результаты в нужном формате. Кроме того, некоторые продвинутые инструменты предлагают такие опции, как макросы для повторяющихся задач, что еще больше повышает производительность.

При выборе инструмента обратите внимание на такие функции, как выбор базы и пошаговое преобразование, чтобы получить точные результаты. Независимо от того, нужно ли вам преобразовать двоичную систему в десятичную или шестнадцатеричную в десятичную, эти инструменты помогут вам справиться с процессом преобразования без проблем. Не забудьте скопировать и вставить результаты или воспользоваться функцией экспорта, чтобы сохранить работу.

Преобразование чисел как текста в обычные числа

В сфере управления цифровыми данными работа с числовыми значениями, представленными в виде текста, требует точных методов преобразования их в функциональные числа. Этот процесс включает в себя интерпретацию текстовых представлений чисел в различных базах, таких как двоичная, десятичная или шестнадцатеричная, и преобразование их в числовые аналоги. Такие преобразования крайне важны для точных вычислений и обработки данных.

2. Процесс преобразования обычно начинается с анализа текста и определения основания используемой в нем системы счисления. Например, число может быть выражено в шестнадцатеричном или двоичном формате. После определения основания применяется формула для преобразования текстового представления в число с основанием 10. Каждая цифра или символ в тексте обрабатывается в соответствии со своим основанием, после чего производятся вычисления для получения окончательного числового значения.

В практических приложениях эта задача может быть решена с помощью различных инструментов и методов. Например, вы можете использовать конвертер или калькулятор для автоматического преобразования. Некоторые инструменты позволяют ввести число в виде текста и указать основание, а инструмент выполняет необходимые вычисления для получения числа в десятичном формате. Аналогичным образом, продвинутые макросы и сценарии могут автоматизировать этот процесс для больших наборов данных или повторяющихся задач.

3. Важно отметить особенности различных базисов. Например, в 12-радиксной системе используются символы, выходящие за пределы обычного диапазона 0-9. При конвертации таких чисел обязательно используйте конвертер, способный работать с этими уникальными характеристиками. Многие онлайн-ресурсы и программное обеспечение предоставляют функции, позволяющие легко справляться с подобными преобразованиями.

4. Чтобы получить пошаговый подход, следуйте следующим рекомендациям: Начните с вставки текста в соответствующее поле конвертера. Убедитесь, что основание правильно установлено в соответствии с форматом числа. Инструмент отобразит преобразованное число, часто в формате base-10. Если вы работаете вручную, используйте метод деления и остатка, чтобы вычислить эквивалентное десятичное значение с поправкой на позиционное значение основания.

Помните, что независимо от используемого метода, точность определения основания и преобразования очень важна. Для получения дополнительных рекомендаций и практических инструментов воспользуйтесь соответствующими онлайн-ресурсами и калькуляторами и всегда проверяйте правильность результатов.

p.s. Для выполнения специфических задач и индивидуальных требований рассмотрите возможность использования специализированного конвертера оснований или внедрения макроса, адаптированного под ваши нужды. Такой подход позволит упростить процесс преобразования и повысить эффективность.

Преобразование текстовых чисел в стандартные числовые форматы

Преобразование текстовых представлений чисел в стандартные числовые форматы включает в себя ряд систематических шагов, которые соответствуют различным числовым базам. Этот процесс необходим для перевода чисел, записанных в одной базе, в другую, что обеспечивает их полное понимание и использование в практических приложениях.

При выполнении таких преобразований можно использовать несколько методов. Например, чтобы перевести число из двоичного формата в десятичный, каждая цифра двоичного числа умножается на степень двойки, соответствующую ее позиции. И наоборот, при преобразовании из десятичной системы счисления в двоичную происходит деление десятичного числа на два и отслеживание остатков. Аналогичным образом можно преобразовывать восьмеричные и шестнадцатеричные форматы, где каждая цифра умножается на соответствующую мощность основания.

Чтобы упростить эти преобразования, существует множество бесплатных инструментов. Конвертер или калькулятор может автоматизировать процесс, предоставляя простой в использовании интерфейс, в котором пользователь может ввести число в определенном основании и получить результат в нужном формате. Например, текстовое поле ввода может принимать значения в различных базах, а результаты преобразования отображаются в виде таблицы для наглядности.

Использование таких инструментов не только повышает точность, но и экономит время за счет минимизации ручных вычислений. В общем, преобразование чисел из одного текстового представления в другое облегчается пониманием правил, характерных для конкретной базы, и использованием соответствующих инструментов преобразования для получения эффективных результатов.

Метод 1. Зеленый угол индикатора

Метод Green Indicator Corner предлагает инновационный подход к преобразованию чисел из одного числового представления в другое. Этот метод использует визуальный индикатор для упрощения процесса преобразования, делая его доступным и удобным для пользователя. Благодаря использованию специального визуального сигнала пользователи могут эффективно управлять различными числовыми форматами и с легкостью манипулировать ими.

При таком подходе конвертер оснащен зеленым уголком, который выделяет соответствующие области ввода и вывода. Этот метод особенно эффективен при работе с десятичными, двоичными и восьмеричными форматами. Для начала достаточно ввести исходное число в специальную ячейку конвертера. Затем инструмент обрабатывает это значение и представляет результат в заданном целевом формате.

Для более четкого понимания выполните следующие действия:

Введите число: введите числовое значение в поле ввода конвертера.
Выберите формат: Выберите нужное основание или систему (например, двоичную, восьмеричную, десятичную).
Просмотреть результаты: В зеленом углу будет выделено преобразованное значение в выбранном формате, что обеспечит мгновенную обратную связь.

Этот метод удобен для тех, кому требуется быстрая и точная конвертация, и доступен бесплатно через различные онлайн-инструменты. Дополнительные ресурсы, нажмите здесь чтобы узнать больше о функциях и возможностях конвертера.

Метод 2. Повторное вхождение

Повторный ввод — это простой подход к конвертации между различными системами счисления. Этот метод предполагает многократный ввод данных в конвертер или калькулятор для достижения желаемого результата. Этот процесс может показаться ручным, но он позволяет выполнять точные и гибкие преобразования между различными системами счисления.

Чтобы эффективно использовать этот метод:

Выберите подходящий конвертер: выберите подходящий инструмент, поддерживающий системы счисления, с которыми вы работаете. Для этого существует множество бесплатных онлайн-калькуляторов.
Введите число: Введите число в том основании, в котором оно находится в данный момент. Например, если вы начинаете с десятичного числа, введите его в поле ввода конвертера.
Выберите целевое основание: Укажите основание, в которое вы хотите преобразовать число. Обычно выбирают двоичную, восьмеричную, десятичную и шестнадцатеричную системы.
Выполните преобразование: Запустите процесс преобразования, нажав соответствующую кнопку или опцию в инструменте. Результат будет отображен в выбранной системе счисления.
Повторяйте по мере необходимости: Если вам нужно выполнить несколько преобразований, вам может потребоваться повторно ввести разные числа и повторить описанные выше шаги. Такой подход может быть полезен при работе с различными наборами данных.

Советуем прочитать: Как определить, есть ли у человека тюремное прошлое

Одним из примечательных аспектов этого метода является его адаптивность. Он позволяет выполнять простые и точные преобразования, не требуя дополнительных настроек или специализированного программного обеспечения. Например, преобразование десятичного числа в шестнадцатеричное, а затем в двоичное может быть выполнено простым повторным вводом в конвертер.

P.S. Если вам часто приходится преобразовывать числа, подумайте о создании макроса или сценария для автоматизации повторяющихся задач. Это поможет сэкономить время и сократить количество ошибок при ручном вводе.

Метод 3. Формула

При преобразовании чисел между различными числовыми базами одним из эффективных подходов является использование метода, основанного на формулах. Этот метод предполагает использование математических выражений, которые позволяют преобразовать число из исходного основания в другое. Этот процесс может выполняться вручную или с помощью различных онлайн-инструментов, автоматизирующих эти вычисления.

Чтобы проиллюстрировать это, рассмотрим число, представленное в десятичном формате. Чтобы перевести это число в двоичную, восьмеричную или любую другую систему счисления, можно применить специальные формулы. Например, при переводе десятичного числа в двоичное вы многократно делите его на 2 и записываете остаток. Аналогично, при переводе в восьмеричное число нужно делить на 8. Каждый шаг в этих вычислениях представляет собой мощность основания, в которое производится перевод, а результат строится из этих значений.

В практических приложениях использование формулы позволяет глубже понять процесс преобразования и может оказаться незаменимым при решении конкретных задач. Чтобы выполнить преобразования вручную, необходимо тщательно следовать этим шагам, обеспечивая точность каждого вычисления. Для тех, кто предпочитает автоматизированный подход, существует множество конвертеров, которые применяют эти формулы за кулисами, чтобы быстро получить результат. Понимая основные принципы, вы сможете лучше использовать эти инструменты и эффективно проверять их результаты.

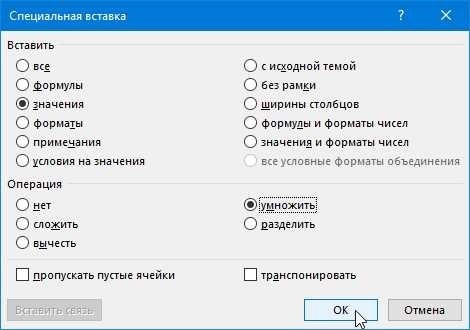
Метод 4. Специальная вставка

В области преобразования чисел специальная вставка предлагает эффективный подход к работе с различными числовыми системами. Этот метод особенно полезен, когда вам нужно работать с числами в разных системах счисления, таких как десятичная, восьмеричная, шестнадцатеричная и другие. Процесс включает в себя использование специального инструмента или техники для упрощения преобразования без ручных вычислений.

Ниже приведено пошаговое руководство по использованию специальной вставки для конвертации:

Шаг 1: Найдите в Интернете надежный инструмент для конвертации. Многие из этих инструментов доступны бесплатно и могут конвертировать числа между различными основаниями.
Шаг 2: Введите базовое значение вашего числа в соответствующее поле ввода. Например, если у вас есть число в десятичном формате, укажите основание как десятичное.
Шаг 3: С помощью специального метода вставки вставьте число в конвертер. Инструмент автоматически определит и обработает значение на основе указанного основания.
Шаг 4: Просмотрите результат, в котором будет показано число, преобразованное в нужное основание. Например, если вы ввели десятичное число, конвертер отобразит эквивалентное восьмеричное или шестнадцатеричное значение.

Этот метод упрощает процесс преобразования, позволяя напрямую вводить и преобразовывать значения без сложных ручных вычислений. Подобные инструменты также часто предоставляют возможность копировать результаты или выполнять дополнительные вычисления.

Для тех, кто интересуется более продвинутыми возможностями, многие конвертеры предлагают дополнительные функции, такие как поддержка различных оснований чисел, настраиваемые параметры и даже пакетные преобразования. Изучите эти функции, чтобы полностью использовать возможности выбранного вами инструмента.

Например, если вам нужно преобразовать число в его шестнадцатеричный или восьмеричный эквивалент, просто выполните описанные выше действия, используя специальный инструмент конвертера. Специальный процесс вставки гарантирует, что каждая цифра будет точно обработана и отображена в правильном формате.

С помощью этого метода преобразование между различными числовыми представлениями становится простым и эффективным. Используйте этот подход, чтобы упростить работу с числами в различных базах.

Метод 5. Текст по столбцам

В этом методе числа преобразуются путем расположения их в столбцах, каждый из которых представляет различные базовые значения. Этот подход особенно полезен для ручных расчетов и понимания тонкостей числовых систем. Он предполагает разбиение числа на составные части и последовательное преобразование этих частей в нужную базовую систему.

Чтобы проиллюстрировать этот метод, рассмотрим следующий пример, в котором мы переводим число из десятичной системы в шестнадцатеричную, используя табличный формат. Мы будем использовать столбцы для представления каждого шага процесса преобразования, что облегчит отслеживание вычислений и проверку результатов.

Шаг	Десятичное число	Шестнадцатеричное значение	Вычисление
1	255	FF	255 / 16 = 15 R 15
2	15	F	15 / 16 = 0 R 15

В этой таблице каждая строка представляет собой шаг в процессе преобразования: десятичное число делится на основание (16 для шестнадцатеричной системы), а остаток преобразуется в соответствующую шестнадцатеричную цифру. Этот метод может быть адаптирован для различных систем счисления, таких как двоичная, восьмеричная и десятичная.

Для более глубокого понимания вы можете найти полезные ссылки и калькуляторы по следующим ссылкам: [Decimal to Binary Converter](#), [Hexadecimal Calculator](#). Используя эти инструменты, вы сможете быстро выполнять преобразования и проверять результаты, полученные ручным способом.

Метод 6. Макрос

Использование макроса — эффективный метод преобразования значений в различных базах, не прибегая к помощи онлайн-конвертеров. Этот метод предполагает создание набора автоматических команд, которые выполняют процесс преобразования за вас. Это обеспечивает точность и последовательность, особенно при выполнении повторяющихся задач. Задавая определенные правила и формулы, макросы позволяют работать с числами в таких форматах, как двоичный, восьмеричный, десятичный, шестнадцатеричный и другие.

По сути, макрос автоматизирует процесс преобразования чисел из одного формата в другой в программной среде. Вы можете запрограммировать эти команды на получение входных значений, применение необходимых преобразований и вывод результатов в нужном вам формате. Такой подход особенно полезен при работе с большими наборами данных или при частом выполнении преобразований, поскольку позволяет минимизировать ручные усилия и потенциальные ошибки.

При создании макроса для преобразования чисел необходимо четко определить правила преобразования. Например, макрос может принимать на вход десятичное число, преобразовывать его в двоичное, а затем в шестнадцатеричное, в зависимости от ваших требований. Использование функций и формул в макросе обеспечивает точность и эффективность преобразования.

Для тех, кто хочет применить этот метод, очень важно понимать синтаксис и возможности языка макросов в выбранном вами приложении, будь то Excel, Google Sheets или другой инструмент. Правильно настроив макросы, вы добьетесь беспрепятственного преобразования числовых значений в различных базах, что сделает ваш рабочий процесс более плавным и продуктивным.

P.S. Всегда тщательно тестируйте свои макросы, чтобы убедиться, что они справляются со всеми возможными ситуациями и дают точные результаты. Это избавит вас от возможных проблем и обеспечит 100-процентную надежность конвертации.

Когда речь идет о преобразовании чисел между различными базами, важно учитывать несколько ключевых аспектов. В этом процессе часто используются различные инструменты и методы, которые помогают преобразовать значения из одного числового формата в другой. Например, десятичная система может быть переведена в двоичный, восьмеричный или шестнадцатеричный формат и наоборот.

Для точного преобразования очень полезно использовать специализированные конвертеры или калькуляторы. Многие из этих инструментов доступны бесплатно и предлагают простой интерфейс для ввода и обработки значений. Конвертеры могут автоматически выполнять преобразование, вычисляя значения остатка и выполняя необходимые арифметические операции.

Также полезно обратиться к внешним ссылки которые содержат дополнительные рекомендации по данной теме. Эти ресурсы часто предлагают подробные объяснения и практические примеры. Среди распространенных методов — калькуляторы преобразования оснований, которые помогают преобразовать десятичные числа в двоичный, восьмеричный или шестнадцатеричный формат и обратно. Кроме того, использование макросов в программных приложениях позволяет оптимизировать повторяющиеся задачи для эффективной обработки.

Помните, что понимание особенностей различных конвертеров и лежащих в их основе процессов очень важно для получения точных результатов. Работаете ли вы с текстом или числовыми значениями, знание этих основ обеспечит правильное и эффективное выполнение преобразований.

Ссылки по теме

В сфере конвертации между различными числовыми системами крайне важно иметь доступ к надежным инструментам и ресурсам. Независимо от того, работаете ли вы с двоичным, восьмеричным, десятичным или шестнадцатеричным форматом, следующие ссылки предоставляют важную информацию и утилиты для беспрепятственного преобразования. В этом разделе вы найдете несколько полезных конвертеров, калькуляторов и пояснительных материалов, которые помогут вам в преобразовании чисел.

Конвертер чисел RapidTables — Комплексный инструмент для преобразования между различными системами счисления, включая двоичную, восьмеричную, десятичную и шестнадцатеричную. Этот ресурс обеспечивает доступ к точным и быстрым преобразованиям.
Конвертеры единиц измерения Конвертер оснований — Этот сайт предлагает простой интерфейс для преобразования между числовыми системами. Конвертер баз поддерживает различные форматы и обеспечивает мгновенный результат.
Калькулятор Суп Конвертер оснований — Полезная утилита для преобразования между различными базами данных. Инструмент обеспечивает четкий вывод результатов и позволяет легко копировать их.
Двоично-шестнадцатеричный конвертер — Специализируется на преобразовании двоичных и шестнадцатеричных форматов, обеспечивая точность и удобство работы.
Mathway Base Converter — Предлагает надежный калькулятор для преобразования различных оснований чисел, включая как распространенные, так и менее стандартные форматы.

Обязательно изучите эти инструменты и используйте их в соответствии с вашими потребностями. Каждый ресурс предоставляет уникальные функциональные возможности и интерфейсы для различных типов преобразований, обеспечивая полный спектр возможностей в вашем распоряжении.